MURNUS
Multiple Uniform Rearranged for Non Uniform Sampling
Multiple Uniform Rearranged for Non Uniform Sampling
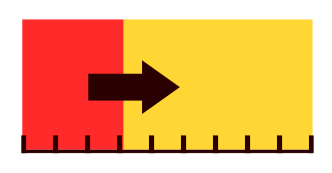Even if sampling rates are far below the Nyquist rate, you'll be able to extend your bandwith and exceed the Nyquist-Shannon limit. Without aliases or ghosts.
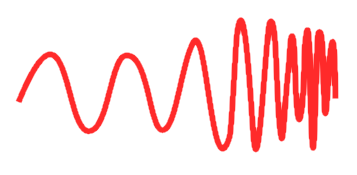Whether they're created, transmitted, echoed, naturally occurring, or whatever... just access them with MURNUS strategy. Don't discard them with a bandpass filter: see what's up there!
No need to pursue expensive, unpractical, ultra-complex, not-available instruments. Perform uniform sampling at normal rates with ordinary devices.
The reconstruction of spectra and signals is easily performed with solid and commonly available Non Uniform Sampling (NUS) algorithms.
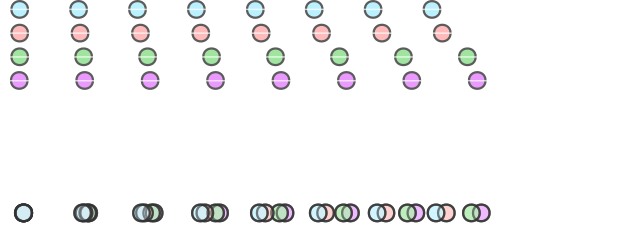
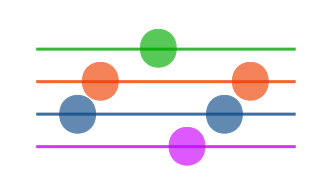Regular uniform sampling is performed multiple times, each time with a (slightly) different sampling rate.
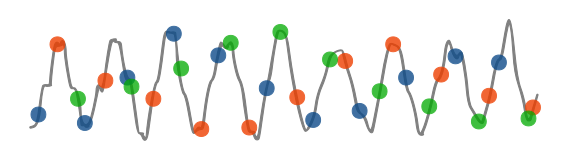
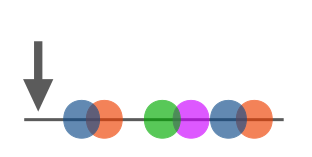At the core of MURNUS, all the separate acquisitions are merged together. This leads to exceptionally small distances between points, artificially rising the overall sampling rate.
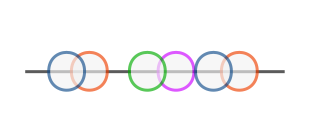Eventually, the data is processed as if it was collected at once in a single acquisition. Due to the irregular distribution of the points a Nonuniform Sampling (NUS) algorithm is used.